Comparing Autoregressive Time-Series Models to Forecast GDP
I’m currently taking an intro to econometrics course this semester. Over the last two weeks, the topic was about time-series regressions. Although I’m pretty skeptical about the ability of mankind to predict the future, it’s quite fascinating to see how much money analysts and forecasters in big firms can make in a year. So, I decided to take it a shot.
In this article, we will discuss briefly about the most basic time-series econometrics models called autoregressive models. We will also learn a little bit about data management in STATA, especially for time-series data. Our objective here is to learn STATA by example, and hopefully, we will be able to figure out how these models would perform against each other using the data of world countries’ GDP.
Preparing our data
The first thing we need to do is to download the data from the World Bank website. In this example, I downloaded the Excel format, but CSV will also do.
Before we start, make sure that our workspace is clean.
clear all
Then, load the Excel file using import excel command.
// load the gdp dataset
import excel "PATH_TO_DOWNLOADED_EXCEL_FILE.xls", sheet("Data") cellrange(A4) firstrow case(lower)
Our data lives inside an Excel sheet called Data, and the column names are placed in the 5th row. Combining the cellrange and firstrow option provides us with the correct labels for our data.
Let’s also remove some variables that we won’t use in this project, just to clean things up a little bit.
// remove unnecesary variables
drop countryname indicatorname indicatorcode
Let’s take a look at our data.
| countrycode | e | f | g | h | … |
|---|---|---|---|---|---|
| ABW | . | . | . | . | … |
| AFE | 2.113e+10 | 2.162e+10 | 2.351e+10 | 2.805e+10 | … |
| AFG | 5.378e+08 | 5.489e+08 | 5.467e+08 | 7.511e+08 | … |
| AFW | 1.045e+10 | 1.117e+10 | 1.199e+10 | 1.273e+10 | … |
| ARG | . | . | 2.445e+10 | 1.827e+10 | … |
| AUS | 1.861e+10 | 1.968e+10 | 1.992e+10 | 2.154e+10 | … |
| AUT | 6.593e+09 | 7.312e+09 | 7.756e+09 | 8.374e+09 | … |
Each row contains the data of a country’s GDP over time. To do the regression, we want to restructure our data so that each row holds the data of each country’s GDP at a single point in time. To do this, we need to rename our columns so that we can identify the year in which the data point was recorded.
foreach v of varlist * {
local x : variable label `v'
// rename the variable name if the variable label name is all digit
// so that we don't rename the countrycode variable
if uisdigit("`x'") rename `v' gdp`x'
}
| countrycode | gdp1960 | gdp1961 | gdp1962 | gdp1963 | … |
|---|---|---|---|---|---|
| ABW | . | . | . | . | … |
| AFE | 2.113e+10 | 2.162e+10 | 2.351e+10 | 2.805e+10 | … |
| AFG | 5.378e+08 | 5.489e+08 | 5.467e+08 | 7.511e+08 | … |
| AFW | 1.045e+10 | 1.117e+10 | 1.199e+10 | 1.273e+10 | … |
| ARG | . | . | 2.445e+10 | 1.827e+10 | … |
| AUS | 1.861e+10 | 1.968e+10 | 1.992e+10 | 2.154e+10 | … |
| AUT | 6.593e+09 | 7.312e+09 | 7.756e+09 | 8.374e+09 | … |
Then, let the reshape command do all the heavy lifting for us.
reshape long gdp, i(countrycode) j(year)
(j = 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 197
> 5 1976 1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991
> 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007
> 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022)
Data Wide -> Long
-----------------------------------------------------------------------------
Number of observations 266 -> 16,758
Number of variables 64 -> 3
j variable (63 values) -> year
xij variables:
gdp1960 gdp1961 ... gdp2022 -> gdp
-----------------------------------------------------------------------------
Now, we have transformed our table into panel data with variables called year (time) and countrycode (entity). This panel data format makes switching between countries a breeze. However, in this article, we’re only interested in forecasting one country at a time.
Here is our data after transformation.
| countrycode | year | gdp |
|---|---|---|
| SGP | 1960 | 7.048e+08 |
| SGP | 1961 | 7.646e+08 |
| SGP | 1962 | 8.262e+08 |
| SGP | 1963 | 9.176e+08 |
| … | … | … |
| IDN | 1967 | 5.668e+09 |
| IDN | 1968 | 7.076e+09 |
| IDN | 1969 | 8.337e+09 |
| IDN | 1970 | 9.151e+09 |
| … | … | … |
Crafting our models
As I have previously mentioned, we’re going to use the autoregressive time-series model. In a nutshell, this model says that a time series variable, which in this case is GDP, is a function of its own lagged values.
The equation above shows the AR(1) model where a country’s GDP depends on its own past value, specifically one year before. We can also extend this model to the point where the GDP is a function of, not only its own value from the year before, but also its own value from two years back.
This is called the AR(2) model, and you can always add more of the lagged values as long as they are good at predicting your dependent variable . Later in this article, we will discuss some of the goodness-of-fit measures we can use to compare these two regression models, namely R-squared and adjusted R-squared.
Let’s start with the AR(1) model. This model tries to predict the value of given . Therefore, we need to generate our variable, which is the previous year’s GDP for each observation.
sort countrycode year
by countrycode: gen lag1_gdp = gdp[_n-1]
(3,626 missing values generated)
| countrycode | year | gdp | lag1_gdp |
|---|---|---|---|
| SGP | 1960 | 7.048e+08 | . |
| SGP | 1961 | 7.646e+08 | 7.05e+08 |
| SGP | 1962 | 8.262e+08 | 7.65e+08 |
| SGP | 1963 | 9.176e+08 | 8.26e+08 |
| … | … | … | … |
| IDN | 1967 | 5.668e+09 | . |
| IDN | 1968 | 7.076e+09 | 5.67e+09 |
| IDN | 1969 | 8.337e+09 | 7.08e+09 |
| IDN | 1970 | 9.151e+09 | 8.34e+09 |
| … | … | … | … |
With this data, we can run our regression model using the reg command. Keep in mind that this dataset contains the data of all countries, so we need to filter the observations we want to include in our regression using if statement.
We can store the country code in a local variable so that we can reuse it in the other commands.
local country = "SGP"
Therefore, changing the country that we want to regress is just as easy as swapping the country variable with a different string value.
Let’s regress our AR(1) model to forecast the Singapore’s GDP.
reg gdp lag1_gdp if countrycode == "`country'"
Source | SS df MS Number of obs = 62
-------------+---------------------------------- F(1, 60) = 5691.82
Model | 1.0516e+24 1 1.0516e+24 Prob > F = 0.0000
Residual | 1.1086e+22 60 1.8476e+20 R-squared = 0.9896
-------------+---------------------------------- Adj R-squared = 0.9894
Total | 1.0627e+24 61 1.7422e+22 Root MSE = 1.4e+10
------------------------------------------------------------------------------
gdp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
lag1_gdp | 1.056428 .0140028 75.44 0.000 1.028418 1.084438
_cons | 1.83e+09 2.23e+09 0.82 0.415 -2.63e+09 6.29e+09
------------------------------------------------------------------------------
There are a lot of numbers here, but right now we’re interested in the R-squared.
shows the variations that can be explained by our variables, which in this case is the , or the previous year’s GDP. As far as I know, the maximum value for a time series data is one. So, we want our to be as close to that number as possible.
Although we are using a very simple model, the result shows that our model has an of our , which is pretty good, I guess.
So, based on our data, Singapore’s GDP at year can be defined as:
To see how well our AR(1) model performs against our current dataset, we can execute the STATA’s predict command to generate our predictions next to our dataset.
predict gdp_hat_ar_1 if countrycode == "`country'"
(option xb assumed; fitted values)
(16,758 missing values generated)
This command creates a new variable called gdp_hat_ar_1 that holds our prediction data. You can ignore the missing values warning, since we know that in some years, the lagged value of the GDP lag1_gdp is not available.
| countrycode | year | gdp | lag1_gdp | gdp_hat |
|---|---|---|---|---|
| SGP | 1960 | 7.048e+08 | . | . |
| SGP | 1961 | 7.646e+08 | 7.05e+08 | 2.57e+09 |
| SGP | 1962 | 8.262e+08 | 7.65e+08 | 2.64e+09 |
| SGP | 1963 | 9.176e+08 | 8.26e+08 | 2.70e+09 |
| SGP | 1964 | 8.942e+08 | 9.18e+08 | 2.80e+09 |
| SGP | 1965 | 9.746e+08 | 8.94e+08 | 2.77e+09 |
| … | … | … | … | … |
Then, we can plot our predictions with the actual data.
line gdp gdp_hat_ar_1 year if countrycode == "`country'"
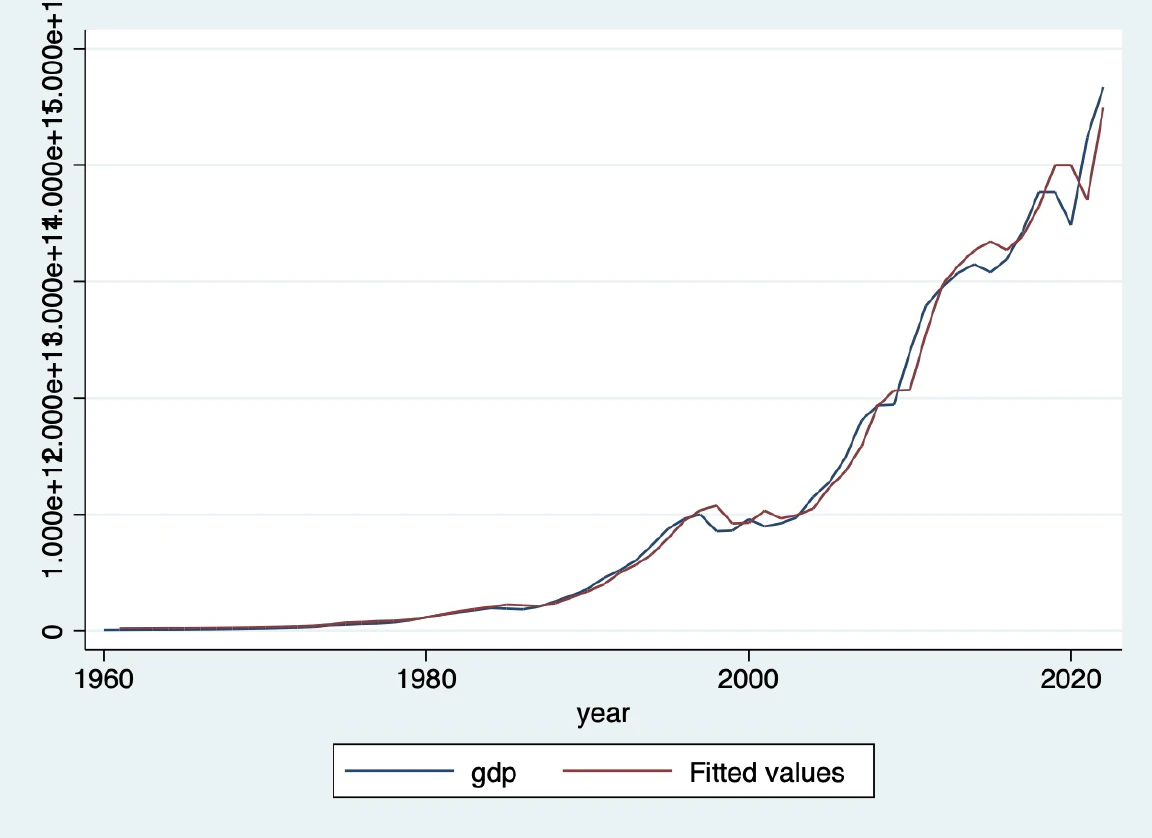
Our prediction (the red line) is pretty much close to the actual data (the blue line), which is exactly what we want.
We can do the same thing for the AR(2) model. Right now, we don’t have the variable that holds the , so let’s use gen command to generate the lagged value for each observation.
by countrycode: gen lag2_gdp = gdp[_n-2]
Then, we can regress the gdp variable against lag1_gdp and lag2_gdp.
reg gdp lag1_gdp lag2_gdp if countrycode == "`country'"
Source | SS df MS Number of obs = 61
-------------+---------------------------------- F(2, 58) = 2735.87
Model | 1.0399e+24 2 5.1997e+23 Prob > F = 0.0000
Residual | 1.1023e+22 58 1.9006e+20 R-squared = 0.9895
-------------+---------------------------------- Adj R-squared = 0.9891
Total | 1.0510e+24 60 1.7516e+22 Root MSE = 1.4e+10
------------------------------------------------------------------------------
gdp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
lag1_gdp | 1.129971 .1329956 8.50 0.000 .8637519 1.396191
lag2_gdp | -.0783055 .1404113 -0.56 0.579 -.3593693 .2027583
_cons | 1.80e+09 2.30e+09 0.79 0.435 -2.79e+09 6.40e+09
------------------------------------------------------------------------------
So, our AR(2) model looks pretty much like this:
To compare these models more comprehensively, we can use some help from estout, a STATA package that we can use to make a side-by-side comparison of our two regression outputs. Let’s install the package using the ssc command.
ssc install estout, replace
Then, we can re-run our regressions and save our estimation results as ar_1 for the AR(1) model and as ar_2 for the AR(2) model.
eststo ar_1: reg gdp lag1_gdp if countrycode == "`country'"
eststo ar_2: reg gdp lag1_gdp lag2_gdp if countrycode == "`country'"
Finally, print the regressions table. Here, we add the r2 and ar2 options to display the R-squared and the adjusted R-squared of both regressions, mtitles to display the name of our regressions at the top, and label to make use of the variable labels.
esttab, r2 ar2 mtitles label
----------------------------------------------------
(1) (2)
ar_1 ar_2
----------------------------------------------------
lag1_gdp 1.056*** 1.130***
(75.44) (8.50)
lag2_gdp -0.0783
(-0.56)
Constant 1.82981e+09 1.80415e+09
(0.82) (0.79)
----------------------------------------------------
Observations 62 61
R-squared 0.990 0.990
Adjusted R-squared 0.989 0.989
----------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001
We can see that our adjusted R-squared drops slightly from to after adding the second lag value to our original model. Notice that we use adjusted R-squared instead of R-squared when comparing models with two or more variables since R-squared naturally decreases as you include more variables in your regressions. Does the slight difference in the adjusted R-squared make the AR(2) slightly worse than the AR(1) model? I have no idea.
However, it’s interesting to see the coefficient of our lagged value is not significant, even at a 95% confidence level. You can tell by the number of stars after the coefficient, three stars means that it is significant at 99.9%, two stars means it is significant at 99%, and so on. This means that the additional lag we put in our model doesn’t really help explain the actual GDP data in our dataset.
Conclusion
Based on our observations, we can see that the AR(1) model is already sufficient to predict the actual data in our dataset. However, this doesn’t always mean that the model can accurately predict Singapore’s 2023 GDP. In the real world, forecasters use insanely more complicated models that take into account many other variables, and even those are still prone to extraordinary events like a global pandemic or sudden raise in geopolitical tension that could potentially mess up their predictions.
It’s also important to point out that our results only apply to Singopore’s GDP data. Different countries might yield different results. Nonetheless, feel free to play around with the do-file, and let me know if you find something interesting!
Here is the complete do-file of this project.
clear all
// load the gdp dataset
import excel "/PATH_TO_FILE/API_NY.GDP.MKTP.CD_DS2_en_excel_v2_5994847.xls", sheet("Data") cellrange(A4) firstrow case(lower)
// remove unnecesary variables
drop countryname indicatorname indicatorcode
foreach v of varlist * {
local x : variable label `v'
// rename the variable name if the variable label name is all digit
// so that we don't rename the countrycode variable
if uisdigit("`x'") rename `v' gdp`x'
}
// transform data into panel data format
reshape long gdp, i(countrycode) j(year)
// add lagged values (GDP n-1 and GDP n-2) for each country,
// we need to group by country code first, otherwise the
// lagged values from the previous country get shifted
// to next country
sort countrycode year
by countrycode: gen lag1_gdp = gdp[_n-1]
by countrycode: gen lag2_gdp = gdp[_n-2]
// set the country code we want to forecast
local country = "SGP"
// regress the GDP data with AR(1) model, and save the result as ar_1
eststo ar_1: reg gdp lag1_gdp if countrycode == "`country'"
// generate prediction data (y hat) for our AR(1) model
predict gdp_hat_ar_1 if countrycode == "`country'"
// regress the GDP data with AR(2) model, and save the result as ar_2
eststo ar_2: reg gdp lag1_gdp lag2_gdp if countrycode == "`country'"
// generate prediction data (y hat) for our AR(2) model
predict gdp_hat_ar_2 if countrycode == "`country'"
// compare the R-squared and adjusted R-squared the two models
esttab, r2 ar2 mtitles label
// visualize our model compared with the real-world data
line gdp gdp_hat_ar_1 year if countrycode == "`country'"
line gdp gdp_hat_ar_2 year if countrycode == "`country'"
My thoughts on STATA
From a programmer’s standpoint, STATA is definitely not the best programming I have ever worked with. I don’t understand why economists around the world, including my professors and lecturers, think of it as the holy grail of econometrics. The loop is terrible, variables are sometimes created implicitly without notice, and there is no way for me to interact with low-level APIs like making HTTP requests and so on.
However, it is worth appreciating how fast and easy it is for someone who doesn’t come from a software development background to pick up this language. As far as I know, back in the old days, most econometrics models were only available in STATA but not in other tools. So I think we’re just stuck with it today, just like the software development world is stuck with NULLs and segfaults.
Tags: Econometrics, Forecast, Time-Series